神のお告げ

2013年05月07日

　ある日のこと、初等科を訪ねてきた卒業生が独り言のように呟いていました。
「なぜ垂直二等分線を引くのか分かりません。」
　初めは何のことか、何を言っているのか、分かりませんでした。でも、よく話を聞いてみると、初等幾何の、
「二等辺三角形の底角が等しいことを証明せよ。」
という問題についてでした。

　頂点Ａの角の二等分線ＡＤを引き、二つの三角形ＡＢＤとＡＣＤ
で考えると、二辺夾角が等しいので合同であることが分かります。だから、底角Ｂと底角Ｃは等しいとなります。

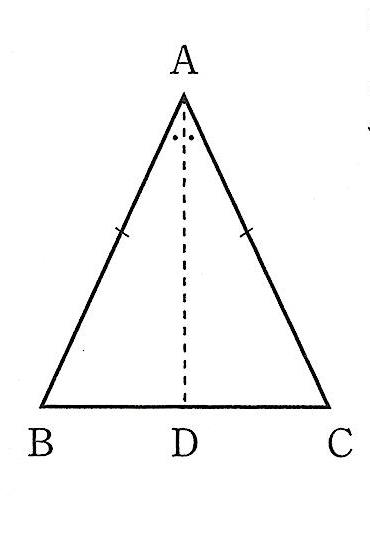
　このとき結果において角ＡＤＢと角ＡＤＣは等しいので直角になり、ＡＤは辺ＢＣの垂直二等分線であるということが分かります。

　では、初めからこの垂直二等分線を証明に使えないだろうか、と考えてみます。

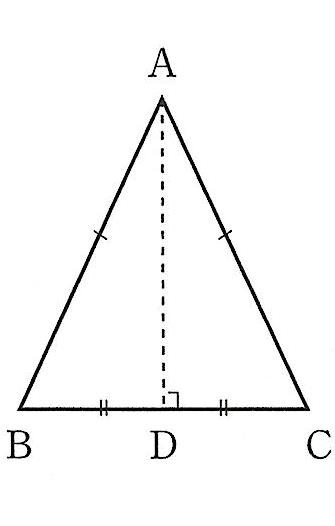
　これが使えると話は簡単です。辺ＡＢとＡＣは等しく、辺ＢＤとＣＤも等しい。辺ＡＤは共通で等しい。だから、三辺が等しいので合同である、といえます。
　しかし、辺ＢＣの垂直二等分線ＡＤは、いつでも頂点Ａを通るといえるのでしょうか。不安がつきまといます。

　このようにみてくると、この問題を解く鍵は補助線ＡＤにあることが分かります。
　では、この補助線ＡＤを引くアイディアはどこから出てくるのでしょうか。
　予習をしてきて、この解法をとうとうと述べている生徒に、なぜこのアイディアを思いついたのか、と訊ねても合点の行く答えは返ってきません。教科書に書いてあったから、参考書に書いてあるから、と歯切れの悪い返答だけが返ってきます。なかには、
「昔から決まっているから」
「第六感から」
「神のお告げだから」
などとうそぶく人もいます。神のお告げがないと手も足も出ないのでしょうか。

　大きさを比べるとき重ね合わせてみます。右手と左手を重ね合わせて、同じ大きさであると確信するときの手法です。

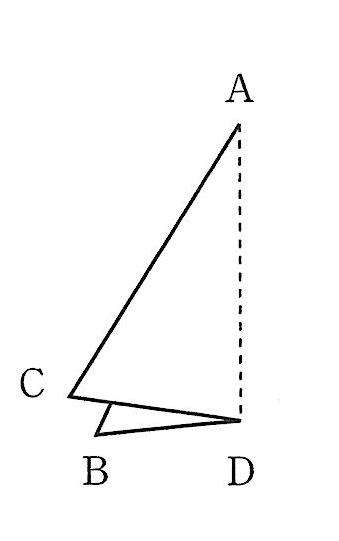
　二つの底角ＢとＣを重ね合わせてみると、ぴったりと重なり合うのです。このときの折り目の線ＡＤが補助線ＡＤなのです。これは神のお告げではなく、日常的なアイディアの活用なのです。日常的なアイディアを生かし、自分の考えを持てる初等科生になってほしいと思います。